In this post we introduce the second of the three predictors of self-categorization: normative fit.

First though, do you remember the context for this? We are talking about the factors that determine which social groups and social categories come to be self-defining for us. Last post introduced comparative fit, which we summarized as follows:

The principle of comparative fit is that we are more likely to believe that a collection of stimuli represents a group or category to the degree that the observed distances between those stimuli are on average less than the observed distances between that collection of stimuli and other stimuli in the frame of reference.

You might also remember the below figure, which we used to demonstrate the idea of comparative fit and meta-contrast. Put in broad terms, we were talking about how the categorization schemes that we adopt reflect patterns present in the environment that surrounds us.

On the left we found square-like shapes vs. triangle-like shapes to be a meaningful categorization scheme based on comparative fit. On the right, where the ‘frame of reference’ was extended, we found straight shapes vs. round shapes could be an alternative meaningful categorization scheme.

Got it? Great; we are making swift progress. Just two more to go before we have all three predictors of self-categorization under our belt.

Normative fit

An intuitive way of thinking about normative fit is this: where comparative fit is concerned with the category structure (i.e. where category boundaries are and where stimuli fall in relation to those boundaries),[1] normative fit is concerned with category content.

Fleshing this out, normative fit is concerned with role of stimuli features in determining the characteristics that we ascribe to cognitive categories. What do we mean by this? Well conveniently we have just seen normative fit in action. Look back for a second at our four example categories from last week. Through comparative fit we ended up with the categories square-like, triangle-like, straight shapes, and round shapes. Now look at the names of the categories. How did we come up with these? Enter normative fit.

These names are, of course, a reflection of the shared features of the stimuli. The category square-like contains stimuli that all bear a resemblance to squares, the category triangle-like contains stimuli that all bare a resemblance to triangles, and so on. What we are seeing here is simply the features of category members driving our understanding of the category.

That’s normative fit in a nutshell, and we can summarise normative fit as follows:

The principal of normative fit is that the content of the cognitive categories we use to understand stimuli will reflect the features of category members and the dimensions on which those stimuli are categorized.

Now, that was quick and easy, but there is a potential problem here…

The problem is that the normative fit principal could come across as somewhat redundant. After all, we were perfectly able to come up with our category names during our discussion of comparative fit. More than that, it wouldn’t have even been possible to talk about comparative fit without also acknowledging the dimensions of comparison. Why then the separate principal? Why not just leave normative fit as an implicit aspect of comparative fit?

It turns out that there are two good reasons to separate normative fit from comparative fit, despite the fact that they are inextricably intertwined. The first of these is reasonably straight forward; the separation helps highlight category content as something that we should be concerned about. Take leadership for example. Yes, category structure is critical for leadership; who we include and who we exclude in our self-categories goes a long way toward determining who we are influenced by. We also need, however, an awareness of self-category content. Just what are the characteristics that define the psychological ingroup, or what it means to be ‘us’? These will determine the ingroup members from the outgroup members.

Moreover, category content will determine of the success or failure of particular influence attempts. Aspiring leaders can only expect to move people in directions that are not substantial violations of ingroup norms and stereotypes. Don’t expect the IT department to suddenly all take up rubgy, union members to turn around and vote liberal, or vegans to be easily convinced to have a steak dinner. Awareness of social category content keeps us realistic about the limits of our leadership potential.

The second reason for the separation is that normative fit links our experience of stimuli with our beliefs and expectations. Or in other words, normative fit is a point of connection with perceiver readiness. This is a more complex idea. Fortunately for us, however, there is a classic normative fit study that helps us convey this point.

In laboratory research Penny Oakes, John Turner and Alex Haslam randomly allocated research participants into one of six experimental conditions.[2] In these conditions they presented participants with a film where three arts students and three science students discussed university life. In reality these students were actors, and the researchers determined in advance the attitudes that each student would take to university life; these attitudes were either pro-‘social life’ or pro-‘hard work’. These were the discussion patterns orchestrated by Oakes and colleagues:

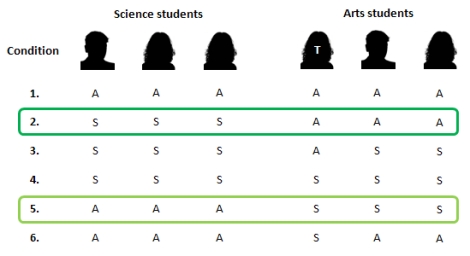
In the notation here ‘A’ equals a pro-‘social life’ attitude (i.e. a position stereotypical to arts students) and ‘S’ equals a pro-‘hard work’ attitude (i.e. a position stereotypical to science students)

As you can see, by varying the pattern of attitudes the researchers have manipulated both comparative and normative fit. In terms of normative fit, which we are concerned with here, the difference between conditions 2 and 5 is the most illustrative. In these conditions comparative fit is equivalent. That is, in both discussions the three science students take the same position while the three arts students take the alternate position. What is different is normative fit. In condition 2 the pattern of attitudes are in line with the expectations we would have for the content of a ‘science students vs. arts students’ categorization scheme. In contrast, in condition 5 the pattern is backwards; the science students are taking a stereotypically artsy position and the arts students are taking a stereotypically sciencey position.

What does this mean for categorization? Well amongst the results of the study Oakes and colleagues found something pretty neat. When they asked participants how similar one of the arts students was to the other arts students (student T, above) they found that in condition 2 the student was seen as more similar to the rest of the arts students than in condition 5. Now remember, there is equivalent comparative fit in these two conditions and in both cases the arts students are all agreeing with one another. Why the difference in perceived similarity then? What is going on?

The answer lies is a combination of two points. First, similarity is an outcome of categorization, and second, perceivers bring with them expectations about what categorization schemes make sense.

What has happened is that the science students vs. arts students categorization scheme was interrupted in condition 5 by the poor normative fit; the content didn’t match participant expectations. Further, the potential alternative (i.e. fun loving science students vs. hard working arts students) didn’t sit well with participants either. This was therefore also rejected and the participants continued to look for other categorization schemes to make sense of the situation. In terms of similarity, the absence of an inclusive social category for the arts students in condition 5 led to reduced perceived similarity among those arts students, at least in comparison to condition 2 where that inclusive social category was present.

This is what we mean by the connection between normative fit and perceiver readiness. What Oakes and colleagues demonstrated was that for any potential categorization scheme the stimuli, or people in our case, must act in a way that that is normatively fitting. Or more broadly, potential categorization schemes are influenced by our prior knowledge and experiences.

With that all said we now have a reasonably complete introduction to normative fit. Further, having raised the topic of perceiver readiness we now have a perfect segue on to our next post. Excellent.

Expect further details on perceiver readiness and what role it plays in self-categorization very soon. We will essentially be answering the question, how do perceivers influence whether they see themselves in terms of race, religion, nationality, political beliefs, occupation, employer, work team, sports team, etc? See you then.

[1] In fact, the original name given to comparative fit was ‘structural fit’.[3]

[2] Oakes, P. J., Turner, J. C., & Haslam, S. A. (1991). Perceiving people as group members: The role of fit in the salience of social categorizations. British Journal of Social Psychology.

[3] Oakes, P. J. (1987). The salience of social categories. In J. C. Turner, M. A. Hogg, P. Oakes, S. Reicher & M. S. Wetherell (Eds.), Rediscovering the social group: A self-categorization theory (pp. 117-141). Oxford: Basil Blackwell.